Güncel
Çin merkezli MingYang, rüzgar enerjisi sektöründeki liderliğini göstermeye devam ediyor. Firma, son zamanlarda d...
Sodyum, lityuma kıyasla daha bol miktarda bulunmasıyla dikkat çekiyor ve batarya teknolojileri bu potansiyeli ke...
Giysilerimizin yıkandığında boyutlarının küçülmesi, genellikle üzücü bir deneyim olabilir. Ancak tüm giysileri, ...
Avusturya’nın Linz şehrinde bulunan Johannes Kepler Üniversitesi’nden araştırmacılar, avuç içi boyut...
Güney Kore’nin Pohang Bilim ve Teknoloji Üniversitesi’nden bir ekip, su altında ilerleyebilen ve ger...
Patriot füze sistemleri, balistik füzeleri ve hava tehditlerini etkisiz hale getirmek için kullanılan bir hava s...
Rezonans, bir nesnenin veya sistemin, belirli bir frekansta titreşim yapması durumudur. Bu titreşim, nesnenin ve...
Barut, patlayıcı bir madde olan ve tarih boyunca önemli bir rol oynayan bir maddedir. Barut, patlama enerjisi sa...
Nötron bombası, nükleer bir silah olarak kullanılan ve özellikle nötron radyasyonu yayarak büyük bir etki yarata...
Sodyum aljinat, doğal olarak deniz yosunlarının hücre duvarlarından elde edilen bir polimerdir. Bu polimer, gıda...
Havacılık ve uzay mühendisliği, havacılık ve uzay sektörlerinde kullanılan teknolojilerin tasarımı, üretimi ve g...
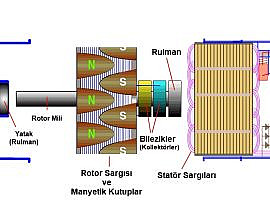
Doğru akım jeneratörleri, elektrik enerjisini doğru akıma dönüştüren cihazlardır. Bu cihazlar, manyetik alanın d...
Refrakter malzemeler genellikle aşağıdaki ana gruplara ayrılır: Refrakter Malzeme Performansı Refrakter malzemel...
Enerji verimliliği, bir sistem, cihaz veya işlemin belirli bir çıktıyı elde etmek için ne kadar enerji kullandığ...
Neuralink’in canlı yayınında, ilk insan denemesi olarak seçilen 29 yaşındaki Noland Arbaugh’un beyin...